LAS ESCUELAS DE EFESO Y ELEA
Después de los pitagóricos aparecieron las dos figuras más importantes del pensamiento presocrático: HERÁCLITO DE EFESO y PARMÉNIDES DE ELEA. Estos dos filósofos también buscaron el fundamento de la naturaleza. Estas dos escuelas fueron opuestas.
¨ HERÁCLITO DE EFESO (540 – 480 a C)
Este filósofo estudió la naturaleza teniendo como base los datos que dan los sentidos. De acuerdo a la observación del proceso evolutivo de la naturaleza y de los seres vivientes llegó a la conclusión de que todo se mueve, todo fluye, nada permanece inmóvil y fijo, todo cambia y se modifica. Este descubrimiento Heráclito lo resumió en su frase más famosa: “nadie se baña dos veces en el mismo río.
Al cambio que sufre la naturaleza Heráclito le dio el nombre de devenir. Este devenir, o cambio, ocurre por la lucha de contrarios, ya que sin oposición ninguna vida es posible. Sin hambre no hay saciedad, sin fatiga no hay reposo, la muerte es impensable sin la vida, y viceversa.
Para Heráclito la característica fundamental del devenir puede entenderse y explicarse a través de esta característica. Para Heráclito el símbolo del cambio eterno o devenir de las cosas es el fuego, el más variable de los elementos.
¨ PARMÉNIDES DE ELEA (540 – 470 a C) Si para Heráclito el fundamento de la realidad era el cambio, para Parménides el fundamento es el ser que no cambia.
Parménides se dio cuenta que todas las cosas que existen tienen en común el mismo hecho de existir, es decir, el ser. Las rocas tienen ser, es decir, son, las plantas son, el hombre es, … El ser no se agota en cada una de las cosas, sino que las cobija a todas. Por ejemplo, el término hombre se aplica a todas las personas, por muy distintas que sean y aunque cambien radicalmente. Por eso se habla del ser humano. Llegó, en sus investigaciones a la conclusión de que el que sabe que el ser existe es el hombre, ya que lo descubrió gracias a su capacidad de pensar, por eso todo lo que uno piensa y dice, es. Por lo tanto, el Pensar y el ser son lo mismo. El ser es inmutable, no tiene principio ni fin; es uno, continuo y macizo, pues lo que es no deja de ser y de lo que no es no puede surgir nada. El ser es eterno, no ha sido creado y existirá siempre, sin cambios.
¨ ZENON DE ELEA (490 – 430 a C)
Fue el discípulo más importante de Parménides, cuyas ideas defendió mediante las aporías (reducción del absurdo de las tesis que intentaba demostrar). sostuvo la inmutabilidad y unicidad del ser. El movimiento sólo existe en el mundo ilusorio de los sentidos.
ACTIVIDAD
.1. Realiza un cuadro comparativo con las similitudes y diferencias de Heráclito y Parmenides.
2. ¿ Con quien estás de acuerdo y por qué?
3. Exposición y argumentación de trabajos
. Es decir, el área del cuadrado grande también es el área del cuadrado pequeño más 4 veces el área del triángulo:
.
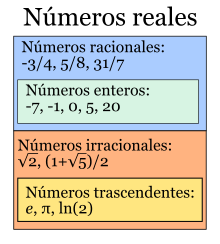
, que se define como la relación entre la longitud de la circunferencia y su diámetro.
, utilizado por artistas de todas las épocas (Fidias, Leonardo da Vinci, Alberto Durero, Dalí,..) en las proporciones de sus obras.
