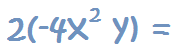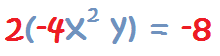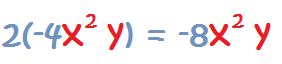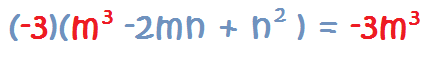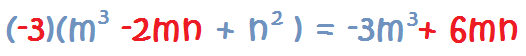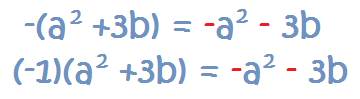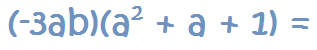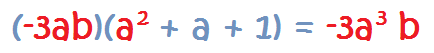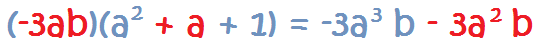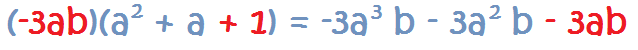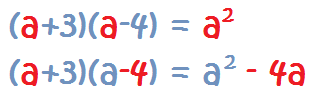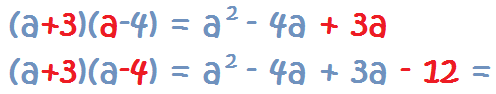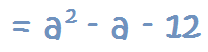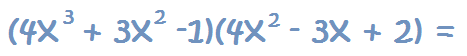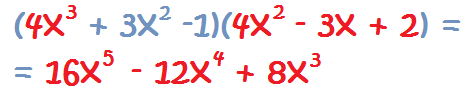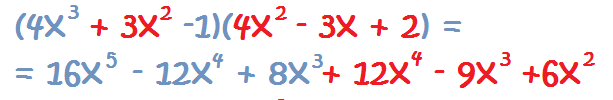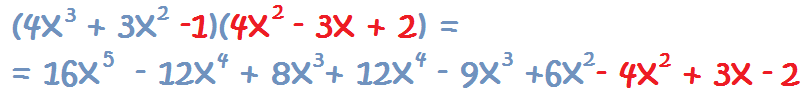23 al 27 de julio
Cómo Multiplicar un Número por un Monomio
Este es el caso más simple. Se procede igual que para multiplicar dos términos, pero en este caso, uno de los dos términos sólo es un número.
Por tanto, se multiplican los números y las variables del monomio se quedan tal y como están en el monomio.
Por ejemplo:
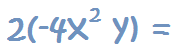
2. Las variables y los exponentes del monomio se quedan igual:
Cómo Multiplicar un Monomio por un Monomio
Recordamos que un monomio es un polinomio de un solo término.
Por eso, multiplicar dos monomios, es lo mismo que multiplicar dos términos y se procede igual que hemos explicado anteriormente para multiplicar dos términos.
Como ya sabes, los términos de un polinomio se componen de un coeficiente (número y signo) y de la parte literal(variables elevadas a sus exponentes).
Para multiplicar dos términos, se sigue este procedimiento:
1. Se multiplican los
coeficientes de cada término, igual que si se tratara de
multiplicar números enteros, teniendo en cuenta la regla de los signos.
2. Para multiplicar la
parte literal de cada término, hay que
tratarlas como una multiplicación de potencias con distintas bases: para las variables que sean iguales, se mantiene la base y se suman los exponentes y las que no sean iguales se quedan tal y como están en el resultado. Vamos a verlo más despacio como sería el procedimiento con un ejemplo:
En esta multiplicación de potencias tenemos dos bases x e y:
Ahora para las potencias que tengan la misma base, se suman los exponentes: x por un lado e y por otro lado:
Vamos a ver otro ejemplo de cómo multiplicar los términos de un polinomio, con términos que también tengan coeficiente:
En primer lugar, multiplicamos los coeficientes, igual que se multiplican los
números enteros:
Ahora vamos con la parte literal. En este caso, tenemos 3 bases: a, b y c. (Aunque las variables no aparezcan elevadas a ningún exponente, en realidad su exponente es 1). Por tanto, para las bases que sean iguales, se suman sus exponentes, igual que en el ejemplo anterior:
Cómo Multiplicar un Número por un Polinomio
Para multiplicar un número por un polinomio, se multiplica el número por cada uno de los términos del polinomio.
Veamos un ejemplo paso a paso:
1. Se multiplica el número por el primer término del polinomio:
2. Se multiplica el número por el segundo término del polinomio:
3. Se multiplica el número por el tercer término del polinomio:
Si tuviéramos más términos, habría que seguir así sucesivamente.
Signo Menos Delante de un Polinomio entre Paréntesis
Un caso particular de un número por un polinomio es el de un signo menos delante de un polinomio entre paréntesis.
Es equivalente a multiplicar por -1:
Como puedes observar, el signo menos cambia de signo los términos del polinomio original. Ésta es una buena forma de acordarse a la hora de eliminar paréntesis cuando estemos operando.
Cómo Multiplicar un Monomio por un Polinomio
En este caso, tenemos que multiplicar el monomio por cada uno de los términos del polinomio, igual que hemos hecho antes. Es decir, es ir multiplicando monomio por monomio repetidas veces.
Por ejemplo:
1. Se multiplica el monomio por el primer término del polinomio:
2. Se multiplica el
monomio por el
segundo término del polinomio:
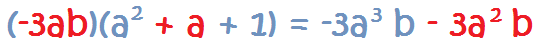
3. Se multiplica el monomio por el tercer término del polinomio:
Multiplicación de Polinomios. Polinomio por Polinomio
Ya hemos llegado al caso más complicado para aprender cómo se multiplican polinomios. Aquí tienes que multiplicar cada término de un polinomio por todos los términos del otro polinomio, es decir:
- Se multiplica el primer término de un polinomio, por todos los términos del otro polinomio
- Se multiplica el segundo término de un polinomio, por todos los términos del otro polinomio
- Se multiplica el tercer término de un polinomio, por todos los términos del otro polinomio
- Y así sucesivamente…
- Se reagrupan términos, sumando y restando los términos semejantes
Vamos a ver algunos ejemplos:
1. Multiplicamos el primer término del primer polinomio, por todos los términos del segundo polinomio:
2. Ahora, multiplicamos el segundo término del primer polinomio, por todos los términos del segundo polinomio:
3. Agrupamos los términos semejantes:
Cuando multiplicamos
dos binomios iguales (que es el cuadrado de un binomio), en vez de desarrollarlos mediante la multiplicación, se utilizan para ahorrar tiempo las
fórmulas de productos notables y llegar al resultado más directamente. Por ejemplo:
(a+b)(a+b) = (a+b)² = a² + 2ab + b²
Ya para terminar, veamos el ejemplo de multiplicar dos polinomios con tres términos cada uno:
1. Multiplicamos el primer término del primer polinomio por todos los términos del otro polinomio:
2. Multiplicamos el segundo término del primer polinomio por todos los términos del otro polinomio:
3. Multiplicamos el tercer término del primer polinomio por todos los términos del otro polinomio:
Multiplicación de polinomios con coeficiente fraccionario.
Procedimiento:
1) Ordenar los términos de los factores cuando sea necesario.
2) Multiplicar los factores, colocando los términos de los productos parciales debajo de su término semejante.
3) Los productos de los coeficientes deben simplificarse.
___________________________________________________
Ejemplos:
a) Multiplicar ½ x² -⅓xy por ⅔x -⅘y
½ x² -⅓xy
⅔x -⅘y .
⅓x³ – ²∕₉x²y
– ²∕₅x²y +⁴⁄₁₅xy²
⅓x³ -²⁸⁄₄₅x²y+⁴⁄₁₅xy² Solución.
b) Multiplicar ⅓x²+ ½y²-⅕xy por ¾x²- ½xy- ¼y²
> Ordenando el primer factor:
⅓x²-⅕xy+½y²
¾x²- ½xy- ¼y² .
¼ x⁴ – ³∕₂₀x³y + ³∕₈x²y²
– ¹∕₆x³y + ¹∕₁₀x²y² – ¼ xy³
– ¹∕₁₂x²y ² +¹∕₂₀xy³ -¹∕₈y⁴
¼ x⁴ -¹⁹∕₆₀x³y +⁴⁷∕₁₂₀x²y² – ¹∕₅xy³ -¹∕₈y⁴ Solución.
___________________________________________________
C)Multiplicar:
x – ⅖y por ⅚y + ⅓x
> Ordenando el segundo factor:
x -⅖y
⅓x +⅚y .
⅓x² -²∕₁₅xy
+ ⅚xy -⅓y²
⅓x² +⁷∕₁₀xy -⅓y² Solución.
___________________________________________________
D) ½ x² -⅓xy + ¼ y² por ⅔x -³∕₂y
½ x² -⅓xy + ¼ y²
⅔x -³∕₂y .
⅓x³ – ²∕₉x²y +⅙xy²
– ¾ x²y +½xy² -³∕₈y³
⅓x³ -³⁵∕₃₆x²y +⅔xy² -³∕₈y³ Solución.
___________________________________________________
E) ⅖m²+⅓mn- ½n² por ³∕₂m²+2n²-mn
> Ordenando el segundo factor:
⅖m²+⅓mn- ½n²
³∕₂m²-mn+2n² .
⅗m⁴ + ½ m³n – ¾ m²n²
– ⅖m³n – ⅓m²n² + ½mn³
+ ⅘m²n² + ⅔mn³ – n⁴
⅗m⁴ +¹∕₁₀m³n -¹⁷∕₆₀m²n² +⁷∕₆mn³ – n⁴ Solución.